For a Certain Continuous Function F the Right Riemann

Students were cross section at height. If we partition the interval into n equal pieces x 1 n.

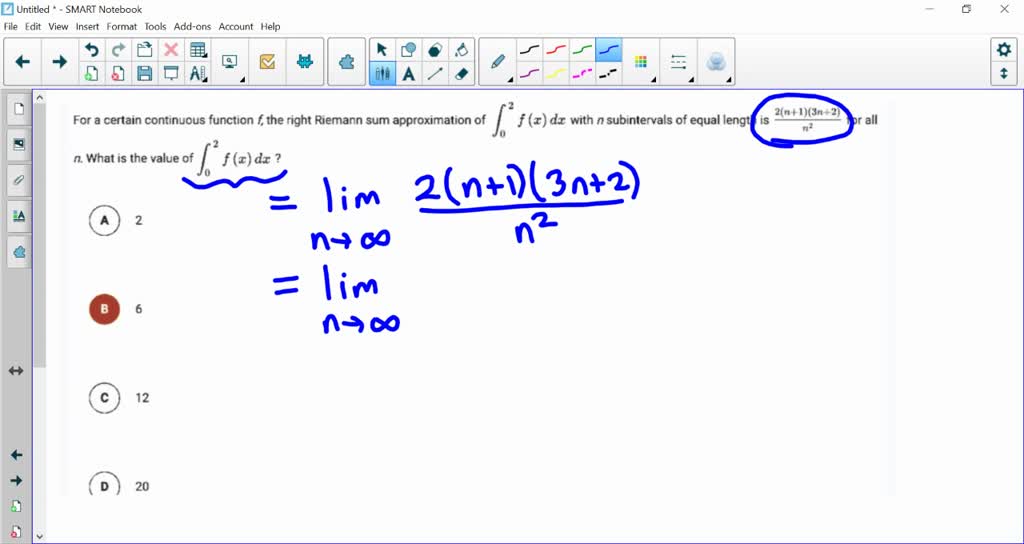
Solved 2 N1 1 3n 2 F Z Dx With N Subintervals Of Equal Length Is For All For Certain Continuous Function F The Right Riemann Sum Approximation Of What Is The Value Of F C

Then use your math.

. I e area under a curve is equal to the The EXAMPLE. So in this question we say for a certain continuous function F. Pandas how to find column contains a certain value Recommended way to install multiple Python versions on Ubuntu 2004 Build super fast web scraper with Python x100 than BeautifulSoup How to convert a SQL query result to a Pandas DataFrame in Python How to write a Pandas DataFrame to a csv file in Python.

If fx f x is a continuous function on ab a b and f f is any antiderivative of fx f x then b a fxdx fbfa. A b f x d x f b f a. The Fundamental Theorem of Calculus FTC summarizes these observations.

A bounded function f. A right Riemann sum uses rectangles whose top- right vertices are on the curve. Which of the sums give an underestimate of the value of Jofx.

A function fis continuous on the closed interval 5 121 and differentiable on the open interval 5 12 and f has the values given in the table above. Endgroup Isochron Oct 15 2021 at 2343. The graph of the function f is shown in the figure above.

For a certain continuous function f the right Riemann sum approximation of Lºsx dx with n subintervals of for all n. Write the following Riemann Sums as definite integrals. Lim Sketch the region corresponding to each definite integral.

What is the value of L x dx. The same thing happens with Riemann sums. Equal length is C 12 D 20 Which ofthe following integral expressions is lim 3k n 1 n.

F x dx found by using a right Riemann sum. Riemann sums for x2. -1 6a - 3a.

A left Riemann sum a right Riemann sum and a trapezoidal sum are used to approximate the value of f x dx each using the same number of subintervals. Riemann Sums Using Rules Left - Right. R a2 - 0.

Fundamental Theorem of Calculus. This result appears for instance as Theorem 611 in Rudins Principles of Mathematical Analysis. Which of the following statements is true.

Riemann sums give better approximations for larger values of n n. Its good to be able to reason about whether a particular Riemann sum is overestimating or underestimating. Let R be the right Riemann sum approximation for f x da using the four subintervals indicated by the data in the table.

If the curve contains the ver ver point 04 then its equation is e2r 4 dx -L clx zx2Cl Yqe x3. The most general antiderivative of cot sec sin x. It is easy to see that the composition of integrable functions need not be integrable.

We dont know how many rectangles are there but for sure the right Riemann sums last rectangle on the right will have its right side as xb because we started drawing rectangles from xb leftwards and so no matter how thin the rectangles are the rightmost rectangles right side is xb. Begingroup The signum function of Thomaes function isnt Riemann integrable but Thomaes function isnt continuous on the rational numbers right. It follows easily that the product of two integrable functions is integrable which is not so obvious otherwise.

Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site. A Riemann sum is defined for f x f x as. Here we look at the right endpoint Riemann sums for fx x2on the interval 0 x 1.

Ab Ris Riemann integrable on ab if its upper integral Uf and lower integral Lf are equal. Before working another example lets summarize some of what we have learned in a convenient way. What is the value of f x dx.

Is a Riemann sum of fx on leftabrighttext Riemann sums are typically calculated using one of the three rules we have introduced. Lim f X dx For a certain continuous function f the right Riemann sum approximation of f x dx with n subintervals of I 311 2 for all n. Overestimation and underestimation When using Riemann sums sometimes we get an overestimation and other times we get an underestimation.

1 3a - a. Up to 24 cash back E There is a number c in the open interval a b such that fc 80. So it is natural to ask whether it works the.

The uniformity of construction makes computations easier. The trapezoidal approximation for 6 0. -3 7a - 6a.

Selected values of f are given in the table above where a is a constant with 0. A296 B 312 C 343 D 374 E 390 _____ 15. Recall that with the left- and right-endpoint approximations the estimates seem to get better and better as n n get larger and larger.

For every real valued continuous function f over a closed interval ab f is also Riemann integrable over ab and that means that the lower and upper integrals are equal and so the answer to this question is that there is no such continuous function. An unbounded function is not Riemann integrable. The function f is continuous on the closed interval 06 and has the values given in the table above.

If a function fis continuous then fis integrable. So in this question they say for a certain continuous function F the right Riemann some approximation of the integral from 0 to 2 of F of x dx with n sub intervals of equal length Is twice the quantity of n plus one times the quantity of three N plus two over and squared for all in. LO 32BEK 32B2 In part c the function f given by 02 503 h fh eh is presented as a model for the area in square feet of the horizontal h feet.

N i1fx iΔx i 1 n f x i Δ x. In the next frame we look at a few Riemann sums. 9 votes Katie Crofton 3 years ago.

Explain that a left Riemann sum approximation for the definite integral of a continuous decreasing function overestimates the value of the integral. In that case the Riemann integral of f on ab denoted by Zb a fxdx Zb a f Z ab f or similar notations is the common value of Uf and Lf. At each point x y on a certain curve the slope of the curve is 4xy.

2n 13n2 equal length is 72 A 2. That the right Riemann some approximation of the integral from 0 to 2 of f of x dx within sub intervals of equal length is twice the quantity of n plus one times the quantity of three M plus two over and squared for all N. Evaluate the definite integral 2xdx using a right-endpoint Riemann sum.

The right endpoints of the intervals are 1 n.

Solved 8 The Values Of A Continuous Function F For Selected Values Of A Are Given In The Table Below What Is The Value Of The Left Riemann Sum Approximation To F Z Dx Using

Solved 20 For A Certain Continuous Function F The Right Chegg Com

Lesson Video Numerical Integration Riemann Sums Nagwa

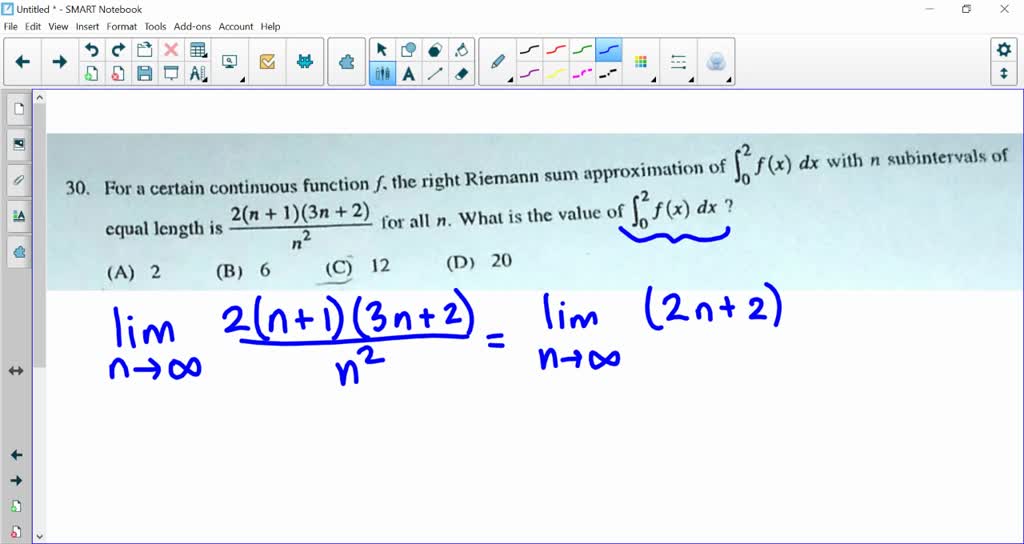
Solved 6 F6 Dx With N Subintervals Of Approximation Of 30 For Certain Continuous Function F The Right Riemann Sum 2 N 1 3n 2 For All N What Is The Value Of

Solved Multiple Choice Course Hero

Solved 20 For A Certain Continuous Function F The Right Chegg Com

Calculus Continuity Foldable Activity Ap Calculus Calculus Ap Calculus Ab

Solved Question 4 0 2 A A3 10a 12a F 3 5 4 2 1 1 12a F X Chegg Com

Solved 6 F6 Dx With N Subintervals Of Approximation Of 30 For Certain Continuous Function F The Right Riemann Sum 2 N 1 3n 2 For All N What Is The Value Of

Graphing Quadratics Graphing Inequalities Calculus

Derivatives Natural Logs And Exponentials Task Card Activities Ap Calculus Ab Task Cards

Riemann Sums And The Definite Integral

Solved Question N Subintervals With Equal Length Explain Chegg Com

Worked Example Finding A Riemann Sum Using A Table Video Khan Academy

Riemann Sums

Solved For A Certain Continuous Function F The Right Chegg Com

Solved 8 The Values Of A Continuous Function F For Selected Values Of A Are Given In The Table Below What Is The Value Of The Left Riemann Sum Approximation To F Z Dx Using

Solved I Need An Explanation About This Question Course Hero

Solved I Need An Explanation About This Question Course Hero